8. Superposition

Written by: Pranav I
Formatted by: Adhulan Rajkamal

Index

8.1 Superposition and interference of waves
8.2 Superposition and stationary waves
8.3 Diffraction and the diffraction grating

8.1 Superposition and interference of waves

Principle of superposition: When two or more waves meet at a point, the resultant displacement at that point is equal to the sum of the displacement of the individual waves at that point
Interference effects can be observed with all types of waves

Constructive and destructive interference

The overlapping of two waves of the same frequency may produce an interference pattern
- Inphase incoming waves interfere constructively
- Antiphase incoming waves interfere destructively
Path difference: The difference between the distances travelled by two waves to reach a point
- Whole number of wavelengths (nλ) → inphase + constructive interference
- Odd number of half-wavelengths (nλ + 0.5λ) → antiphase + destructive interference
- Note: Given that they are inphase in their initial points
Fringes: The maxima and minima disturbances produced due to interference
Interference pattern: The collection of fringes produced by the superposition of overlapping waves

Producing an interference pattern with sound waves

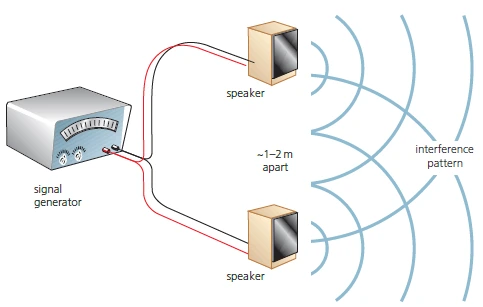
Two loudspeakers connected to the same signal generator to produce waves of the same frequency
Should be done in an open area, on a windless day
The positions of fringes can be detected using a microphone and CRO

Producing an interference pattern with light waves

Two separate light sources, even of the same frequency, produce incoherent waves
Light is emitted as a series of pulses, and there is an abrupt change in phase between each pulse
Coherent waves: Waves with a constant phase difference
Note: same amplitudes are not necessary for observable interference patterns; they just enhance contrast

Young’s double-slit experiment

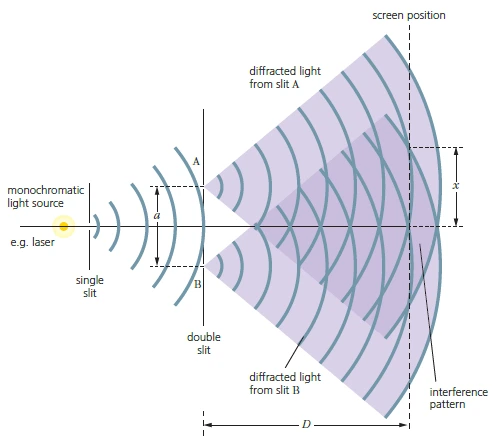
Light waves from slits A and B are coherent since they originate from the same primary source.
Fringe width, x: distance between successive bright or dark fringes

$$ x = \frac{\lambda D}{a} $$

D → distance from the double slit to the screen
a → distance between the centers of the slits
D has to be large (1-2 m) and a has to be small (1-2 mm) since light has very small wavelengths.

Double-slit interference with microwaves

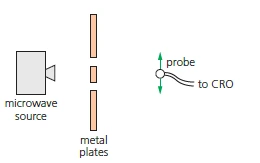
Microwave source emits microwaves of a single frequency
Metal plates produce a double-slit arrangement
Constructive and destructive interference are detected by a microwave probe connected to a CRO
- Can be moved parallel to the metal plates to measure fringe width

The conditions for interference fringes to be observed

Coherent sources have to be used → constant phase difference
If transverse, unpolarized or polarized in the same plane

White light fringes

White light is used in Young’s double-slit experiment
Different wavelengths produce their own fringe pattern
Centre of the pattern → white maxima with black fringes on both sides
A pattern of white fringes with colored edges is formed by maxima and minima of different colors overlapping

8.2 Superposition and stationary waves

Stationary wave: the result of the overlapping and hence interference of two waves of equal frequency and amplitude, travelling along the same line with the same speed but in opposite directions

Stationary waves on strings

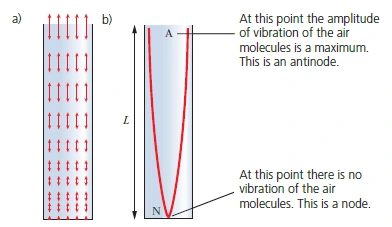
Node: a point of zero amplitude
Antinode: a point of maximum amplitude

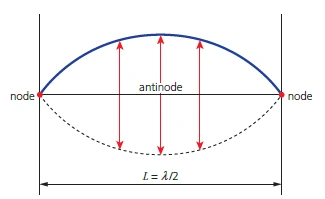
Fundamental node or first harmonic

Wavelength of the fundamental node is $ 2L $.
Therefore, $ f_1 = \frac{c}{2L} $ (where $ c $ is the speed of the progressive waves that interfered to produce the stationary wave).

First overtone or second harmonic

Wavelength $ \lambda = L $.
$ f_2 = \frac{2c}{2L} = \frac{c}{L} $.

Second overtone or third harmonic

Wavelength $ \lambda = \frac{2L}{3} $.
$ f_3 = \frac{3c}{2L} $.

🔥 $ f_n = \frac{n c}{2L} $

This is the general expression for the frequency $ f_n $ of the $ n $th mode (the $ n $th harmonic, or the $ (n-1) $th overtone).

Differences between progressive and stationary waves

Progressive Waves	Stationary Waves
All points have the same amplitude	Amplitude varies with position along the string: it is zero at a node and maximum at an antinode
The wavelength is the distance between adjacent points having the same phase (crest to crest or trough to trough)	The wavelength is twice the distance between adjacent nodes or antinodes
The waveform (crests and troughs) moves with the velocity of the wave	The nodes and antinodes do not move along the string
There is energy translation in the direction of movement of the waveform	There is no translational movement of energy, but energy is associated with the wave
Phase varies continuously along the wave → All neighbouring points are out of phase with each other	Between adjacent nodes, all points vibrate in phase; the particles between two adjacent nodes are 180° out of phase
There are no specific frequency constraints → the wave can have any frequency	Only certain resonant frequencies are possible, depending on the length of the string and the speed of the wave

Explaining the formation of stationary waves

Two waves of the same kind travelling in opposite directions overlap
- Waves have same frequency/wavelength and speed
They form stationary waves

Stationary waves in air

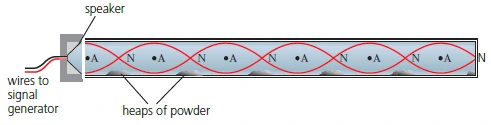
Fig 1.7 Stationary waves in a closed pipe

A fine, dry powder is sprinkled evenly along the tube
While in resonant frequencies:
- The powders settles into heaps at nodes (no disturbance)
- The powder is dispersed in antinodes
In a closed pipe, the closed end has a node and the open end has an antinode
The antinode is slightly outside the open end → the distance is the end-correction

Fundamental mode of vibration of air in a closed pipe

Sound waves are longitudinal, so air particles vibrate as shown in the figure
Wavelength $ \lambda = 4L $
$ f_1 = \frac{c}{4L} $, where $ c $ is the speed of sound in air

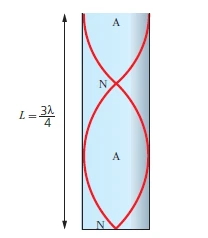
Second harmonic or first overtone

Wavelength $ \lambda = \frac{4L}{3} $.
$ f_2 = \frac{3c}{4L} $.

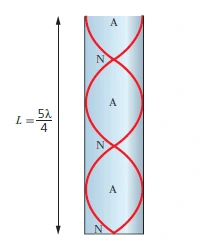
Third harmonic or second overtone

Wavelength $ \lambda = \frac{4L}{5} $.
$ f_3 = \frac{5c}{4L} $.

🔥 $ f_n = \frac{(2n – 1)c}{4L} $

This is the general expression for the frequency $ f_n $ of the $ n $th mode of vibration of air in a closed tube (the $ n $th harmonic, or the $ (n-1) $th overtone).

Measuring the wavelength of stationary waves

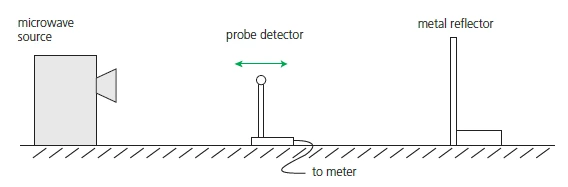
Source of microwaves facing a metal reflecting plate
Stationary waves are produced by interference
Probe detector is placed between the source and the reflector
Position of the reflector is adjusted such that the signal fluctuates regularly as the detector is slowly moved back and forth
$\frac{\lambda}{2}$ = distance between successive minima (nodes) or maxima (antinodes).

Stationary waves using sound

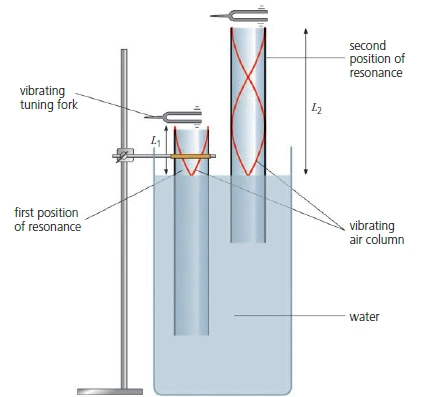
A glass tube is placed in a cylinder of water
A tuning fork or loudspeaker connected to a signal generator is held above the open end of the tube
Tube is gradually raised (increasing $ L $) until a stationary wave is produced (note becomes louder)
First position: $ \frac{\lambda}{4} = L_1 + e $
Second position: $ \frac{3\lambda}{4} = L_2 + e $
$ \frac{\lambda}{2} = L_2 – L_1 $
$ c = 2f(L_2 – L_1) $

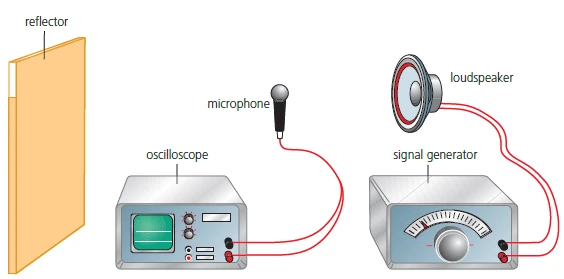
Reflector is moved slowly back and forth until a stationary wave is produced
Microphone is moved along the line between the loudspeaker and the reflector
$\frac{\lambda}{2}$ = distance between successive minima (nodes) or maxima (antinodes)
$ c = 2f d $

8.3 Diffraction and the diffraction grating

Diffraction: The spreading of the wave into regions where it would not be seen if it moved only in a straight line after passing through a narrow split or past an edge
Depends on the width of the gap compared with the wavelength
- Most noticeable when the width is equal to the wavelength
There is no change of wavelength with diffraction

Huygens’ explanation of diffraction

At any instance, all points in a wavefront could be regarded as secondary disturbances
Give rise to their own circular wavelets
The tangent curve of the wavefronts produced by the secondary sources gives the new position of the original wavefront

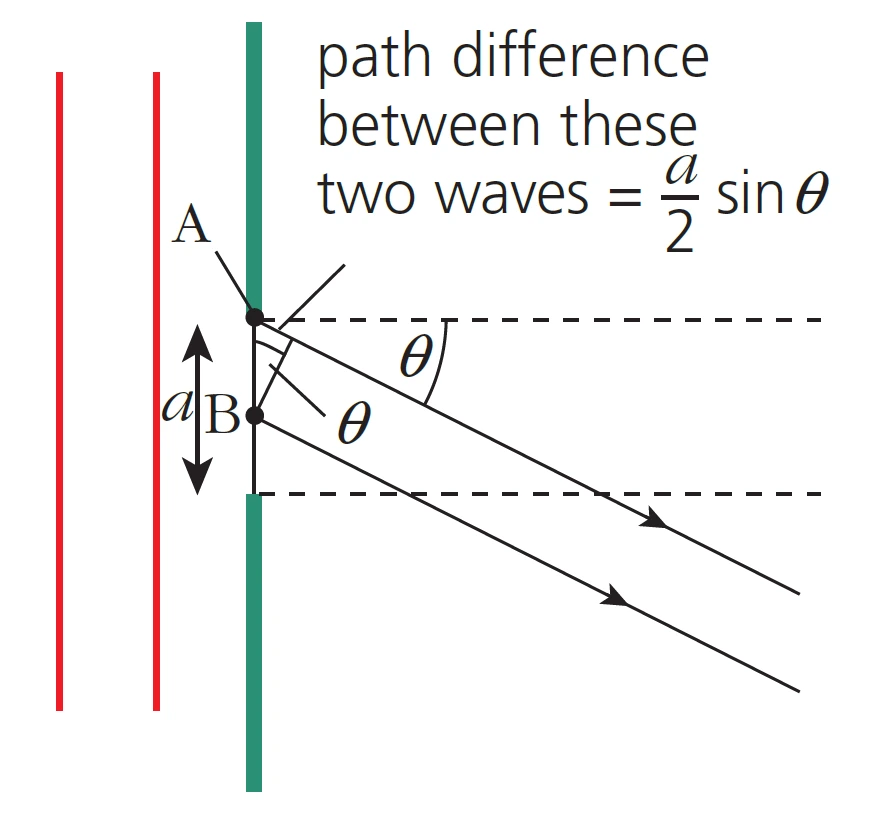
Points A and B (separated by a distance of a/2) are sources of secondary wavelets
Waves from A and B overlap to create an interference pattern

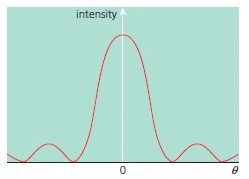
The Diffraction Grating

A plate on which there is a very large number of parallel, identical, very closely spaced slits
Condition for maximum intensity at angle $\theta$:

$$ d \sin\theta = n\lambda $$

$ d $ is the slit spacing and $ n $ is the order (0, 1, 2, 3, …)
Used in a spectrometer

The Diffraction Grating with White Light

Each wavelength making up the white light is diffracted by a different amount

Red light is diffracted by the largest angle
Blue light is diffracted by the least angle

A continuous spectrum is produced at each order
Depending on $ d $, overlapping of orders might occur

AS Level Physics 9702