3. Dynamics

Written by: Pranav I
Formatted by: Adhulan Rajkamal

Index

🔥 Note

Pushing a heavy box at constant speed on a rough surface requires a large force.
When the force of friction gets vanishingly small, the force required to push the object also gets vanishingly small.

Newton’s First Law:
Every object continues in its state of rest, or with uniform velocity, unless acted on by a resultant force.
- Mass is the property of an object that resists change in motion.
Newton’s Second Law:
For an object of constant mass, its acceleration is equal to the resultant force applied to it.
- $ F = ma $ (Force = Mass × Acceleration)
- The direction of acceleration is in the direction of the force.
Newton’s Third Law:
Whenever one object exerts a force on another, the second object exerts an equal and opposite force on the first.
- The two forces act on different objects.
Note: In the exam, you might have to explain Newton’s laws of motion using momentum. (Refer below)

$ p = mv $ (Momentum = Mass × Velocity)
Units → $ \text{kg} \cdot \text{m/s}^{-1} $ or Ns
Newton’s First Law in Terms of Momentum:
The momentum of a particle remains constant unless an external resultant force acts on it.
Newton’s Second Law in Terms of Momentum:
The resultant force acting on an object is equal to the rate of change of its momentum.
- Definition of Force: The rate of change of momentum.
- $ F = \frac{\Delta p}{\Delta t} $, where $ F $ is the resultant force.
Newton’s Third Law in Terms of Momentum:
The rate of change of momentum due to the force on one object is equal and opposite to the rate of change of momentum due to the force on the other object.
- Since the two forces act on each object for the same time, the changes in momentum are equal and opposite.

$ W = mg $, as per Newton’s Second Law of Motion.
It is the effect of a gravitational field on a mass.
The direction of weight is towards the center of the Earth.
Note: Objects at rest and in free fall have the same weight.
A book on a table remains at rest because its weight is balanced by an equal and opposite normal contact force exerted by the table on the book.

These two forces CANNOT be related by Newton’s third law since they are acting on the same object

R and R’ are third-law forces as they are acting on different bodies (R on the book by the table; R’ on the table by the book)
When the book is not on the table:
- Weight of the book → force due to the gravitational attraction of the book by the Earth
- Equal and opposite third-law force → force due to the gravitational attraction of the Earth by the book

Friction acts along the common surface of contact between two objects
- Always acts in the opposite direction to the relative motion of the objects
- Larger for rough surfaces and zero/minimal for smooth surfaces
- Responsible for non-uniform motion
Frictional force in a fluid → viscous force
- Determined by the viscosity (thickness) of the fluid
- Example: air resistance (fluid → air)
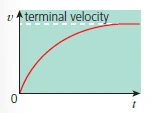
Velocity of an object moving through a resistive fluid eventually reaches a maximum terminal velocity
- Resistive force increases with speed
- Resultant downward force = weight – viscous force
- Resultant force = 0, when the resistive force reaches a value equal and opposite to the weight of the falling object

Important Note: Objects might experience an upward upthrust force when immersed in a fluid, depending on the fluid’s density
- Negligible for air since it has a low density
- Must be considered for more viscous fluids

Principle of conservation of momentum: the total momentum for a system of objects is constant if there is no resultant external force
Thus, an isolated system has constant momentum

As per the principle of conservation of momentum, the total momentum before the collision = the total momentum after the collision

Total momentum before the collision of two objects:
$ m_1 u_1 – m_2 u_2 $
(The negative sign is because $ u_2 $ is in the right-to-left direction.)
Total momentum after the collision of two objects:
$ -m_1 v_1 + m_2 v_2 $
(The negative sign is because $ v_1 $ is in the right-to-left direction.)
Therefore, $ m_1 u_1 – m_2 u_2 = -m_1 v_1 + m_2 v_2 $
Note: Momentum is a vector quantity → take direction into account.

Impulse of a force is equal to the change in momentum.
$ F \Delta t = \Delta p $ (derived from $ F = \frac{\Delta p}{\Delta t} $ → Newton’s Second Law)

Total kinetic energy before the collision of two objects:
$ \frac{1}{2} m_1 u_1^2 + \frac{1}{2} m_2 u_2^2 $
Total kinetic energy after the collision of two objects:
$ \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2 $
If the collision is perfectly elastic, the total kinetic energy before the collision is equal to the total kinetic energy after the collision:
- \[
  \frac{1}{2} m_1 u_1^2 + \frac{1}{2} m_2 u_2^2 = \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2
  \]
- Energy is a scalar → no negative signs.
For a perfectly elastic collision, the relative speed of approach is equal to the relative speed of separation:
$$ u_1 + u_2 = v_1 + v_2$$
Collisions in which the total kinetic energy before and after the collision is not equal are inelastic:
- Kinetic energy is transferred to heat, sound, or other energy forms.
However, total energy and momentum are always conserved (considering no external forces act on the object).