AS Level Chemistry 9701
5. Chemical Energetics
Written by: Adhulan R
Formatted by: Rithanya S
5.1 Enthalpy change (ΔH)
- Chemical reactions are accompanied by enthalpy changes
- Enthalpy (H) → Total energy associated with the materials that react
- We cannot the measure the enthalpy of a compound
- But we can measure the change in enthalpy (ΔH) during a reaction
- Calculating enthalpy change (ΔH):

- Unit of enthalpy change → kJ mol-1
- Enthalpy change (ΔH) can be:
- Exothermic (ΔH is negative)
- Energy lost by reacting species to the surroundings
- Temperature of surrounding increases
- Endothermic (ΔH is positive)
- Energy gained by reacting species from the surroundings
- Temperature of surroundings decreases
- Exothermic (ΔH is negative)
Reaction pathway diagrams
- Diagram showing enthalpy change of a reaction
- Enthalpy change diagram for exothermic reaction:

- Reacting species has lost enthalpy → products have lower energy
- Enthalpy change diagram for endothermic reaction:

- Reacting species has gained enthalpy → products have more energy
Standard conditions
- To make comparison of enthalpy changes fair, we must use the same conditions → standard conditions
- Standard conditions:
- 101 kPa (approx. normal atmospheric pressure)
- 298 K (25°C)
- Each substance is in its normal physical state (standard state)
- Ө → used to indicate that the enthalpy change refers to a reaction carried out under standard conditions
Notice that the symbol Ө shows that this reaction was carried out in standard conditions
Variety of enthalpy changes
- Enthalpy changes can be describe according to the type of chemical reaction taking place:
- Enthalpy change of formation
- Enthalpy change of combustion
- Enthalpy change of neutralisation
- Enthalpy change of reaction (used in general cases)
Standard enthalpy change of reaction (ΔHrӨ)
- ΔHrӨ→ Enthalpy change when the amounts of reactants shown in the balanced chemical equation react to give products under standard conditions – the reactant and products must be in their standard states
- Can be both exothermic or endothermic
- Example:
However, if the equation is balanced so that 2 moles of water is produced – we double the ΔHrӨ
Notice how the unit is no longer kJ mol-1
Standard enthalpy change of formation (ΔHfӨ)
- ΔHfӨ → Enthalpy change when one mole of a compound is formed from its constituent elements under standard conditions. Reactants and products must be in their standard states
- Can be both exothermic and endothermic
- Examples:
- Formula of the compound formed written in square brackets
- State symbol for carbon → graphite (carbon exists in several forms – most stable form used for ΔHfӨ calculation)
- Standard enthalpy change of formation of any element in its standard state is 0
Standard enthalpy change of combustion (ΔHcӨ)
- ΔHcӨ → Enthalpy change when one mole of a substance is burnt in excess oxygen under standard conditions. The reactants and products must be in their standard states
- Always exothermic
- Examples:
⚠️ Note: First equation can be considered as either ΔHcӨ[S(s)] or ΔHfӨ[SO2(g)]
Standard enthalpy change of neutralisation (ΔHneutӨ)
- ΔHneutӨ → Enthalpy change when one mole of water is formed by the reaction of an acid with an alkali under standard conditions
- Example:
- Cl– and Na+ are spectator ions
- Since all acid-alkali reaction have the same ionic equation → same enthalpy change = -57.1 kJ mol-1
Measuring enthalpy changes
- Calorimetry → Technique to measure the enthalpy change of reactions
- Apparatus used → Calorimeter
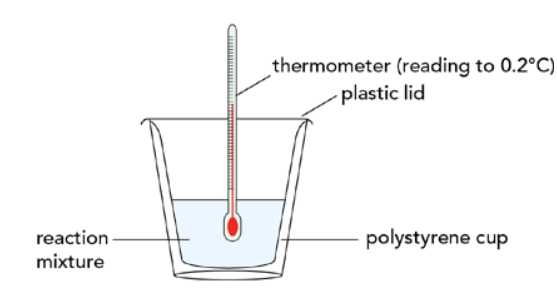
- Known amount of reactants and known volume of liquids used in calorimetry
- Temperature change is measured
- ΔH is calculated using the specific heat capacity of water
- Specific heat capacity, c → Energy required increase the temp. of 1g or 1kg of a substance by 1℃
🔥 Specific Heat Capacity of Water
4.18 kJ kg-1 ℃-1
- Energy transferred as heat is during calorimetry is given by the relationship q = mcT
- q → heat transferred in J
- m → the mass of water in g/kg (depends on what unit is used for the specific heat capacity)
- c → specific heat capacity of water in J g-1 ℃-1 or kJ kg-1 ℃-1
- T → temperature change, in ℃ or K (either can be used – will give the same answer)
- Note: 1 cm3 of water weighs 1 g → we can substitute the volume of water in cm3 for mass of water in g in the equation (unit of specific heat capacity → J g-1 ℃-1)
- Aqueous solutions of acids, alkalis and salts are assumed to be largely water, hence we assume that:
- 1 cm3 of solution has a mass of 1 g (same density as water)
- the solution has the same specific heat capacity as water → 4.18 J g-1 ℃-1 or 4.18 kJ kg-1 ℃-1
- This idea can be scaled up to obtain enthalpy change per mole of defined reactant or product
- Relationship used: H = –mcTn
- n → number of moles of defined reactant or product
- Significance of the negative sign:
- T → has a sign (rise in temp → +ve; fall in temp → -ve)
- Fall in temperature → endothermic → H is +ve
- – –T = +H
- Relationship used: H = –mcTn
Bond energies and enthalpy changes
🔥 Important
- Bond breaking → endothermic
- Energy is required to overcome the attractive forces joining the atom together → energy is absorbed → endothermic
- Bond making → exothermic
- Enthalpy changes occur due to the breaking and forming of bonds
- If energy needed to break bonds is less than energy released to form new bonds → endothermic (vice versa)

- Note: In most reactions only some bonds in the reactants are broken
Bond energy
- Exact bond energy → The energy needed to break a mole of a specific covalent bond in a named molecule in the gaseous state (also called bond dissociation energy or bond enthalpy)
- Symbol for bond energy → E
- We put the type of bond broken in bracket → E(C-H)
- Refers to the bond energy of a mole of single bonds between carbon and hydrogen atoms
- When new bonds are formed the amount of energy released = amount of energy absorbed when the same type of bond is broken
Average bond energy
- Bond energy → affected by other atoms in the molecule
- O-H bond in water has a slightly different bond energy value to the O-H bond in ethanol
- Identical bonds in the same molecule have different bond energies
- Eg: It takes more energy to break the first O-H bond in water than to break the second
- For these reasons → average bond energies taken from a number of bonds of the same type but in different environments
- Average bond energy → The average energy needed to break a specific covalent bond averaged from a variety of molecules in the gaseous state
🔥 Standard enthalpy change of atomisation (HӨat)
- Enthalpy change when one mole of gaseous atoms is formed from its elements under standard condition
- (HӨat)[H2] relates to ½H2(g) → H(g)
5.2 Hess’s law
- Hess’s law → the total enthalpy change in a chemical reaction is independent of the route by which the chemical reaction takes place, as long as the initial and final conditions, including the states of the reactants and products, are the same

- Hess’s law can be illustrated using energy/enthalpy/Hess’s cycle (like the one above)
- H of indirect route 1 = H of direct route = H indirect route 2
- No matter what route is taken to reach product → H is constant
- Hess’s law used to calculate H that cannot be found by calorimetry
Enthalpy change of reaction from enthalpy changes of formation

- Dashed line → indirect route
- Sum of enthalpy changes along the indirect route = enthalpy change of the direct route
- Calculate Hr using this relationship
- Sum of enthalpy changes along the indirect route = enthalpy change of the direct route
- Step by step breakdown:
- Step 1: Write the balanced equation at the top
- Step 2: Draw the cycle with elements at the bottom
- Step 3: Draw in all the arrows, making sure they go in the right directions
- Step 4: Apply Hess’s law (taking into account the number of moles of each reactant and product)
- Example:
- 2NaHCO3(s) → Na2CO3(s) + CO2(g) + H2O(l)
- 2NaHCO3(s) → Na2CO3(s) + CO2(g) + H2O(l)

- Draw enthalpy cycle
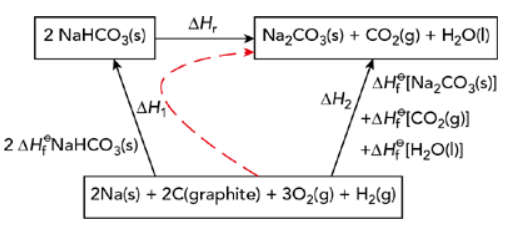
- Apply Hess’s law:
H2 = H1 + Hr
Hr =H2 – H1
Hr =–
- Note the HfӨ[NaHCO(s)] is multiplied by 2 because 2 moles of NaHCO3 appear in the equation
- Insert the values of the standard enthalpy changes (make sure to multiply by the correct number of moles)
Hr =(-1810.0)-(-1901.6) = +91.6 kJ mol-1
- Apply Hess’s law:
🔥 While doing enthalpy cycle calculation remember that
- Hf of an element = 0
- You must take into account the number of moles of reactants and products in each part of the energy cycle
- If there are 3 moles of a substance, eg: 3CO2(g) → we must multiple the enthalpy change of formation by 3
Enthalpy change of formation from enthalpy changes of combustion

- Dashed line → indirect route
- Sum of enthalpy changes along the indirect route = enthalpy change of the direct route
- Calculate Hf using this relationship
- Sum of enthalpy changes along the indirect route = enthalpy change of the direct route
- Step by step breakdown:
- Step 1: Write the equation for the enthalpy change of formation at the top
- Step 2: Add oxygen on both sides of the equation to balance the combustion reactions
- Step 3: Draw the cycle with the combustion products at the bottom (combustion products are always CO2(g) + H2O(l))
- Step 4: Apply Hess’s law (taking into account the number of moles of each reactant and product)
- Example:
- Calculate the standard enthalpy change of formation (HfӨ) of ethane (C2H6)
- Relevant enthalpy changes of combustion are (given information):
HcӨ[C(graphite)] = -393.5 kJ mol-1
HcӨ[H2(g)] = -285.8 kJ mol-1
HcӨ[C2H6(g)] = -1559.7 kJ mol-1 - Draw the enthalpy cycle:

- Apply Hess’s law:
H1 = Hf + H2
Hf = H1 – H2
Hf =2HcӨ[C(graphite)] + 3HcӨ[H2(g)] –HcӨ[C2H6(g)] - Insert the values of the standard enthalpy changes (make sure to multiply by the correct number of moles)
Hf =(-1644.4)-(-1559.7) = -84.7 kJ mol-1
🔥 Note
While constructing enthalpy cycles, the reaction for which Hr is required is put at the top of the cycle triangle
Enthalpy cycle to calculate average bond energy
- Apply Hess’s law to determine H
- Then divide H by 4 (because there are 4 C-H bonds in CH4) → average bond energy
Calculating enthalpy changes using bond energies
- Example: Calculating H for the Haber process
N2(g) + 3H2(g) ⇌ 2NH3(g) - Relevant bond energies (given information)
- Draw the enthalpy cycle:
- Calculate total energy absorbed for bond breaking and released for bond formation (make sure to take into account the number of moles of reactants and products)
Hr=2253 + (-2346) = -93 kJ mol-1
