AS Level Physics 9702
7. Waves
Written by: Adhulan Rajkamal
Formatted by: Adhulan Rajkamal
Index
7.1 Progressive waves
- Wave motion → Transfer energy
- Sources of waves → Vibrating objects
- Progressive waves → Waves which transfer energy from one place to another without transfer of matter
| Vibration of particles at right angles to direction of energy transfer | Vibration of particles parallel to direction of energy transfer |
| Eg: EM waves, surface water waves, and secondary seismic waves (S-waves) | Eg: Sound waves, and primary seismic waves (P-waves) |
Important terms
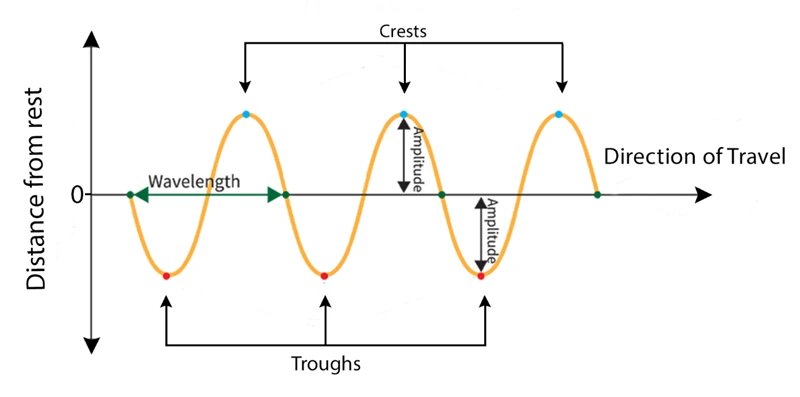
- Displacement (s) → The displacement of a particle in a wave is its distance in a specified direction from its rest/ equilibrium position
- Displacement is a vector quantity → + or –
- Amplitude (A) → maximum displacement of a particle in the wave from its rest/equilibrium position (only the magnitude – hence never negative)
- Phase difference between progressive waves:
- Compares the displacement and relative motion of particles in a wave
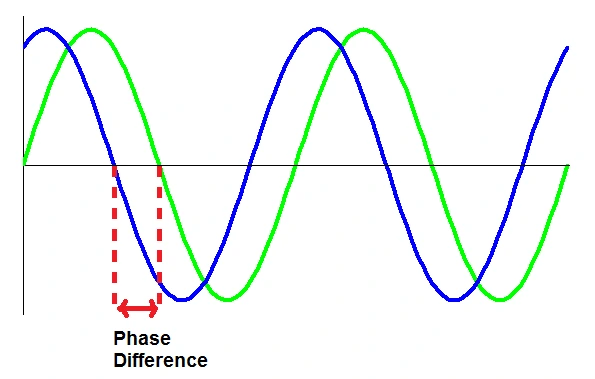
- In-Phase: Two particles vibrate together with the same displacement and motion in the same direction
- Wavefronts: Lines joining points that are in-phase
- Phase Difference: Occurs when crests and troughs of waves do not align
- Anti-Phase: The crest of one wave aligns with the trough of another. Phase difference = \( 180^\circ \) or \( \pi \) radians
- Period (T) → Time taken for a particle to complete one oscillation or cycle
- Frequency (f) → Number of oscillations/cycles per unit time
- Wavelength (\(\lambda\)) → Minimum distance between adjacent crests/troughs
- Distance between two wavefronts → \( \lambda \)
- Speed (v) → Speed of the wave
Wave Equation
- The wave equation → \( v = f\lambda \)
Derivation
- Speed = \( \frac{\text{distance}}{\text{time}} \)
- \( v = \frac{d}{t} \)
- The time taken by a wave to travel a distance equivalent to its wavelength \( (\lambda) \) is its time period \( (T) \)
- Substituting \( d \) with \( \lambda \) and \( t \) with \( T \), we get \( v = \frac{\lambda}{T} \)
- Since \( T = \frac{1}{f} \), substituting \( T \) gives \( v = f\lambda \)
Intensity
- Intensity → Power per unit area
- \( I = \frac{P}{A} \)
- When \( f \) is constant:
- \( I \propto A^2 \) → Intensity is directly proportional to the square of amplitude for a progressive wave
- When \( A \) is constant:
- \( I \propto f^2 \) → Intensity is directly proportional to the square of frequency for a progressive wave
Cathode Ray Oscilloscope
- y-axis → y-gain
- x-axis → time-base
- Example CRO trace:
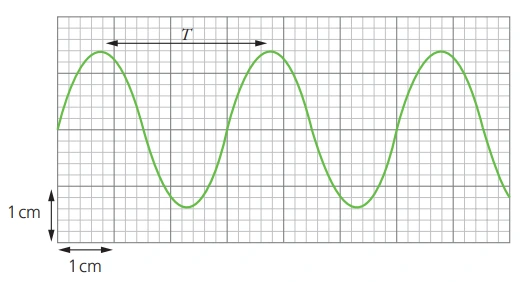
- Both y-axis and x-axis can be calibrated to varying scales
- Calibration will be stated as follows (e.g.):
- Time-base setting is \( \text{2.0 ms cm}^{-1} \)
- Y-gain is \( \text{2.0 V cm}^{-1} \)
- Calibration will be stated as follows (e.g.):
- Use details of the calibration to analyze the CRO trace and perform basic calculations, such as finding the time period
7.2 Transverse and longitudinal waves
| Vibration of particles at right angles to direction of energy transfer | Vibration of particles parallel to direction of energy transfer |
| Eg: EM waves, surface water waves, and secondary seismic waves (S-waves) | Eg: Sound waves, and primary seismic waves (P-waves) |
7.3 Doppler effect for sound waves
- When the source of sound moves relative to a stationary observer → observed frequency \(\neq\) source frequency
- Equation to calculate observed frequency \(\text{f}_o\):
$$\text{f}_o = \text{f}_s \frac{v}{v \pm v_s}$$- \(\text{f}_s\) → source frequency
- \(\text{v}\) → speed of the wave in the medium
- \(\text{v}_s\) → speed of the source relative to the observer
- Source is moving away → Add velocities
- Source is approaching → Subtract velocities
7.4 Electromagnetic spectrum
- All electromagnetic waves are transverse waves that travel with the same speed \( c \) (speed of light → \( 3.0 \times 10^8 \) m/s) in free space.
- Wavelengths of different radiation in the e.m. spectrum (memorise the table):
| Radiation | Wavelength range / \( m \) |
|---|---|
| Gamma rays | \( 10^{-10} – 10^{-16} \) |
| X Rays | \( 10^{-9} – 10^{-12} \) |
| Ultraviolet | \( 10^{-7} – 10^{-9} \) |
| Visible | \( 4 \times 10^{-7} – 7 \times 10^{-9} \) |
| Infrared | \( 10^{-2} – 10^{-6} \) |
| Microwaves | \( 10^{-1} – 10^{-3} \) |
| Radio Waves | \( 10^{4} – 10^{-1} \) |
- Wavelengths in the range \( 400 \)-\( 700 \) nm in free space are visible to the human eye.
7.5 Polarisation
- Polarised wave → Oscillations are confined to a single plane or direction perpendicular to the direction of propagation
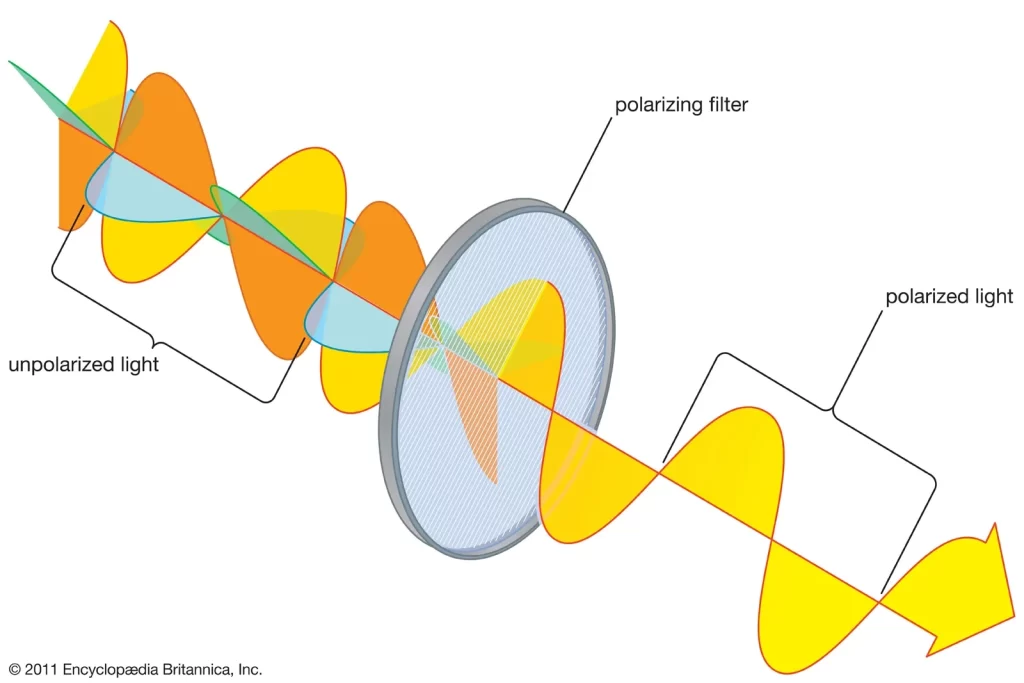
- Polarisation can only occur in transverse waves.
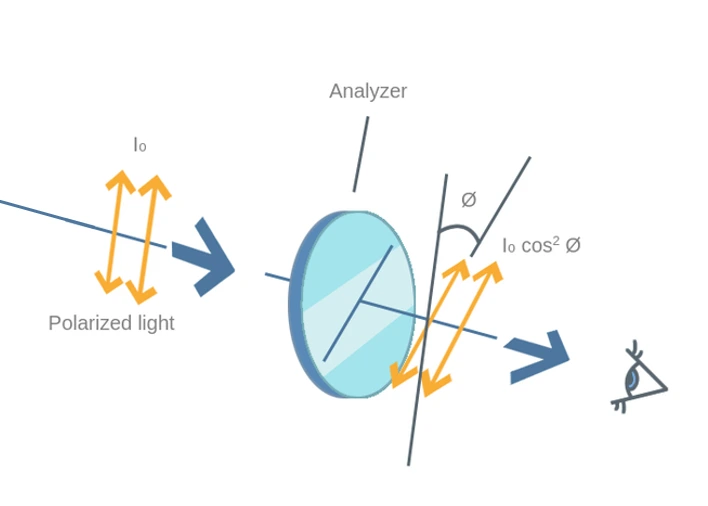
Malus’s Law
- Equation used to calculate the intensity of a plane-polarised e.m. wave after transmission through a polarising filter:
$$ I = I_0 \cos^2 \theta $$
- \( I \) → Intensity of light after passing through the polariser
- \( I_0 \) → Initial intensity of light before passing through the polarising filter
- \( \theta \) → Angle between the light’s initial polarisation direction and the transmission axis of the polariser
🔥 Common mistake
When calculating light intensity through multiple polarisers, always measure \( \theta \)for each filter relative to the polarised light emerging from the previous filter , not the initial light direction
