AS Level Physics 9702
6. Deformation of solids
Written by: Adhulan Rajkamal
Formatted by: Adhulan Rajkamal
Index
6.1 Stress and strain
- Deformation is caused by tensile or compressive forces:
- Tensile → Causes extension
- Compressive → Causes compression
- Load → The external force applied to a material, causing it to deform; measured in newtons (N)
- Weight of the load on a spring → tensile force acting on the spring
- Extension → The increase in length of a material when subjected to a tensile load
- \( \text{Extension} = \text{Stretched Length} – \text{Original Length} \)
- Compression → The decrease in length of a material when subjected to a compressive load (pushing force)
- Hooke’s Law → Provided that the limit of proportionality is not exceeded, the extension of an object is proportional to the applied load
- The law can be expressed as: \( F \propto e \)
- Introducing a constant: \( F = k e \)
- \( k \) is the spring constant, defined as force per unit extension: \( k = \frac{F}{e} \)
- Limit of proportionality → The maximum point up to which the material obeys Hooke’s Law; beyond this point, deformation becomes non-linear
The Young Modulus
- Stress (\( \sigma \)) → The force applied per unit cross-sectional area; measured in pascals (Pa):
\[ \sigma = \frac{F}{A} \]
- F → Force applied (N)
- A → Cross-sectional area (m²)
- Strain (\( \varepsilon \)) → The ratio of extension (or compression) to the original length of a material:
\[ \varepsilon = \frac{e}{L_0} \]
- e → Extension or compression (m)
- L₀ → Original length (m)
- Strain has no units
- Young Modulus (\( E \)) → A measure of the stiffness of a material, defined as the ratio of stress to strain within the proportionality limit
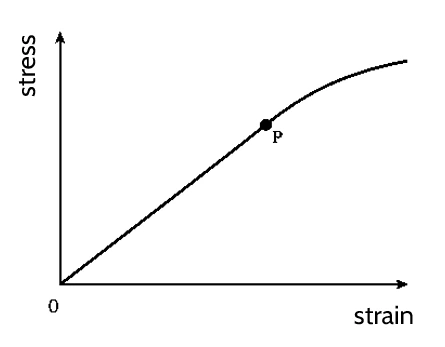
- In the region where the changes are proportional, it can be seen that:
- \(\text{stress} \propto \text{strain}\)
- Adding a constant to remove the proportionality sign: \[ \text{stress} = E \times \text{strain}\]
- The constant \(E\) is known as the Young modulus of the material.
- Rearranging the equation above gives the equation for calculating Young modulus:
\[
E = \frac{\sigma}{\varepsilon} = \frac{F/A}{e/L_0} = \frac{F L_0}{e A}
\]
- Measured in pascals (Pa) → Same unit as stress (\(\sigma\))
- Higher \(E\) indicates a stiffer material
Experiment – Young modulus
- The following setup can be used to perform a simple experiment to measure the Young modulus of a wire.
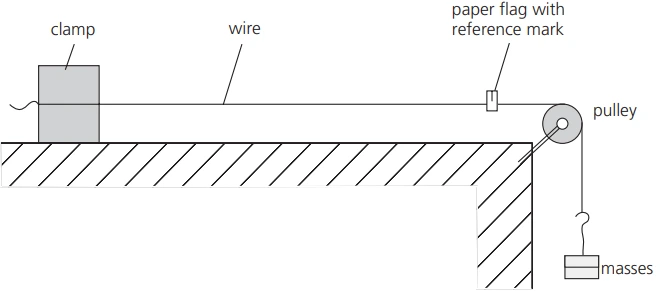
-
- Set-up: A wire is clamped at one end with a load carrier attached to the other; a paper flag marks the reference point.
- Measurements:
- Original length (\( L_0 \)) is measured from the clamp to the reference point.
- Diameter (\( d \)) is measured using a micrometer, and the cross-sectional area is calculated as: \[ A = \frac{1}{4} \pi d^2 \]
- Extension (\( e \)) is measured as masses (\( m \)) are added to the carrier.
- Calculation:
- Load (\( F \)) is found using: \[ F = mg \]
- A graph of \( F \) (y-axis) against \( e \) (x-axis) is plotted (Force-extension graph).
- The Young modulus (\( E \)) is determined from the gradient (\( \frac{F}{e} \)) as: \[ E = \frac{F L_0}{e A} = \frac{F}{e} \times \frac{L_0}{A} = \textit{gradient} \times \frac{L_0}{A} \]
- Note: Ensure the wire does not exceed the limit of proportionality for valid results.
6.2 Elastic and plastic behaviour
- Elastic limit → maximum stress or force that a material can withstand and still return to its original shape and size when the load is removed
- Elastic deformation → Object returns to its original shape and size when the force on it is removed; occurs within elastic limit
- Plastic deformation → Object does not return to its original shape and size when force is removed; occurs when the material is stressed beyond the elastic limit
- Area under force-extension graph represents the work done
- Elastic potential energy of a deformed material = work done to deform the material (within its limit of proportionality)
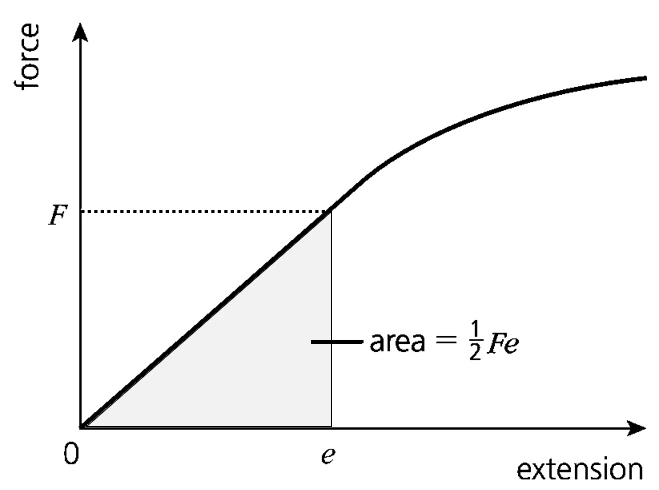
- Equations to calculate the elastic potential energy of a deformed material:
-
\(
E_p = \frac{1}{2} F e
\)
→ Related to the area under the force-extension graph.
- \( F \) → Force
- \( e \) → Extension
-
\(
E_p = \frac{1}{2} k e^2
\)
Where:- \( k \) → Spring constant
- \( e \) → Extension
-
\(
E_p = \frac{1}{2} F e
\)
→ Related to the area under the force-extension graph.
- Derivation of the second equation:
- From the first equation: \( E_p = \frac{1}{2} F e \) and Hooke’s Law: \( F = k e \)
- Substituting \( F = k e \) into the first equation:
\( E_p = \frac{1}{2} (k e) e = \frac{1}{2} k e^2 \)
