AS Level Physics 9702
4. Forces, density and pressure
Written by: Pranav I
Formatted by: Adhulan Rajkamal
Index
4.1 Turning effects of forces
Centre of gravity
- The point where all the weight of the object is taken to act
- For uniform objects, the centre of gravity is at the geometrical centre
Moment of a force
- Product of the force and the perpendicular distance of the line of action of the force from the pivot
- In simple terms, it is the turning effect of a force

- In this case:
- Moment of force \( \neq F \times l \)
- Moment of force \( = F \times d = F \times l \cos \theta \)
- Here, \( l \) is the distance from the pivot, while \( d \) is the perpendicular distance from the pivot.
Couples
- Two forces, equal in magnitude but opposite in direction, whose lines of action do not coincide.
- All these conditions MUST be met for two forces to be called a ‘couple’.

- The turning effect produced is a torque (not a moment since it is produced by two forces)
- ‘F x r’ is the moment produced by a single force about the centre
- Torque = F x 2r (force x perpendicular distance between the forces)
4.2 Equilibrium of forces
The principle of moments
- The sum of clockwise moments about a point equals to the sum of anticlockwise moments about the same point, for the object to be in rotational equilibrium
Equilibrium
- Resultant force is zero (no linear acceleration)
- Resultant moment is zero (no rotational acceleration)
- If these conditions are met, complete equilibrium is achieved
4.3 Density and pressure
Density
- Density is given by: \( \rho = \frac{m}{V} \) (mass per unit volume)
- SI unit: \( \text{kg m}^{-3} \)
Pressure
- Pressure is defined as: \( p = \frac{F}{A} \) (force per unit area)
- \( F \) acts perpendicularly to the area \( A \)
- SI unit: \( \text{N m}^{-2} \) or Pa
Pressure in a Liquid
- The pressure in a fluid increases with depth.
- \( \Delta p = \rho g \Delta h \)
- For an immersed object, the forces due to pressure act perpendicularly to its surface in all directions.
- Absolute pressure = External pressure (e.g. atmospheric) + Pressure due to the depth below the surface of the liquid.
Upthrust
- Immersion in a fluid provides an upthrust or buoyancy force.
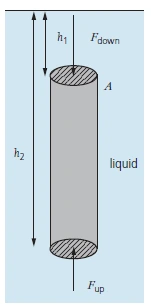
- \( \Delta p = \rho g h_2 – \rho g h_1 \) (difference in hydrostatic pressure due to varying depth)
- Due to the difference in hydrostatic pressure, the force acting upwards on the base of an object is greater than the force acting downwards on the top.
- \( F_b \) (upthrust force) = \( F_{\text{up}} – F_{\text{down}} \)
- \( F_b = \rho g V \) (derived from \( p = \frac{F}{A} \))
- Upthrust is equal to the weight of the liquid displaced by the immersed object.
- The object occupies a volume equal to the volume of the liquid it displaces.
- This is known as Archimedes’ principle.
