2. Kinematics

Written by: Pranav I
Formatted by: Adhulan Rajkamal

Index

Distance: length along the actual path travelled from the starting point to the finishing point
Displacement: length travelled in a straight line in a specified direction from starting point to finishing point
(area under the velocity-time graph)
Average speed: \(\text{average speed} = \frac{\text{distance moved along the actual path}}{\text{time taken}}\)
Average velocity: \(\text{average velocity} = \frac{\text{displacement}}{\text{time taken}}\)
- Instantaneous velocity: rate of change of displacement over an infinitesimally small time period
  (gradient of the tangent to the displacement-time graph)
Acceleration: the rate of change of velocity
(gradient of the tangent to a v-t graph)
\(a = \frac{\Delta v}{\Delta t}\)
Acceleration of free fall: \(9.81 \text{ m s}^{-2}\)

Condition → uniform/constant acceleration
Equation 1: \(v = u + at\)
- Derived from \(a = \frac{v – u}{t}\)
Equation 2: \(s = ut + \frac{1}{2} a t^2\)
- Step 1: \(s = \left(\frac{u + v}{2}\right) t\) (formula for area under a v-t graph)
- Step 2: \(s = \left(\frac{u + (u + at)}{2}\right) t\)
- Step 3: \(s = ut + \frac{1}{2} a t^2\)
Equation 3: \(v^2 = u^2 + 2as\)
- Step 1: \(s = \left(\frac{u + v}{2}\right) t\)
- Step 2: \(2s = t(u + v)\)
- Step 3: \(2s = \frac{(v + u)(v – u)}{a}\)
  - Equation used for substitution: \(t = \frac{v – u}{a}\)
- Step 4: \(2as = v^2 – u^2\)
- Step 5: \(v^2 = u^2 + 2as\)

Results in a parabola (projectile)
Analysed in terms of two independent motions at right angles
- The horizontal component remains constant
- The vertical component increases/decreases by g (acceleration of free fall)

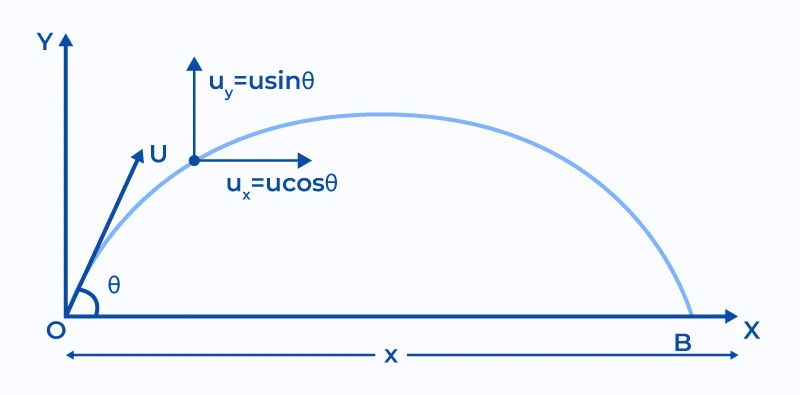
Values of variables:
- \(\theta = 45^\circ\)
- \(U = 20 \text{ ms}^{-1}\)
- \(g = 9.81 \text{ ms}^{-2}\)
Values to be calculated:
- \(h_{\text{max}}\) (maximum height)
- \(x\) (total horizontal distance)
- \(t_{\text{total}}\) (2 × time taken to reach \(h_{\text{max}}\))

Time to Reach Maximum Height (\(t_{\text{max}}\))
Using the equation \(v = u + \Delta t\), with \(v = 0\) at maximum height:
\(t_{\text{max}} = \frac{U_y}{g}\)

Substituting \(U_y = U \sin \theta = 20 \sin 45^\circ = 14.14 \text{ ms}^{-1}\):
\(t_{\text{max}} = \frac{14.14}{9.81} = 1.44 \text{ s}\)

Maximum Height (\(h_{\text{max}}\))
Using the equation \(s = ut + \frac{1}{2} at^2\), with \(a = -g\):
\(h_{\text{max}} = (U_y t_{\text{max}}) – \frac{1}{2} g t_{\text{max}}^2\)

Substituting \(U_y = 14.14 \text{ ms}^{-1}\), \(g = 9.81 \text{ ms}^{-2}\), and \(t_{\text{max}} = 1.44 \text{ s}\):
\(h_{\text{max}} = (14.14 \times 1.44) – \frac{1}{2} (9.81) (1.44)^2\)
\(h_{\text{max}} = 10.2 \text{ m}\)

Total Time of Flight (\(t_{\text{total}}\))
The total time is twice the time to reach the maximum height:
\(t_{\text{total}} = 2 t_{\text{max}} = 2 \times 1.44 = 2.88 \text{ s}\)

Total Horizontal Distance (\(x\))
Using the horizontal motion formula \(x = U_x t_{\text{total}}\), where:
\(U_x = U \cos \theta = 20 \cos 45^\circ = 14.14 \text{ ms}^{-1}\)
\(x = 14.14 \times 2.88 = 40.8 \text{ m}\)

Answers: