AS Level Biology 9700
5. Trigonometry
Written by: Tharun Athreya
Formatted by: Tharun Athreya
5.1 Angles between 0° and 90°
- Trigonometry suggests the relationship between side lengths and angles of triangles.
- The three trigonometric functions Sine, Cosine, and Tangent come from ratios of side lengths in right-angled triangles.
- \( \sin \theta = \frac{\text{OPPOSITE}}{\text{HYPOTENUSE}} \)
\( \cos \theta = \frac{\text{ADJACENT}}{\text{HYPOTENUSE}} \)
\( \tan \theta = \frac{\text{OPPOSITE}}{\text{ADJACENT}} \)- Tip: SOHCAHTOA is an easy way to remember the three basic trigonometry ratios.
| \(0^\circ\) | \(30^\circ\) | \(45^\circ\) | \(60^\circ\) | \(90^\circ\) | |
|---|---|---|---|---|---|
| \(\sin(\theta)\) | \(0\) | \(\frac{1}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{\sqrt{3}}{2}\) | \(1\) |
| \(\cos(\theta)\) | \(1\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{1}{2}\) | \(0\) |
| \(\tan(\theta)\) | \(0\) | \(\frac{1}{\sqrt{3}}\) | \(1\) | \(\sqrt{3}\) | undefined |
5.2 The general definition of an angle
- An angle is a measure of the rotation of a line segment about a fixed point.
- The CAST Diagram:

-
- First quadrant: All graphs are positive between \(0^\circ\) and \(90^\circ\).
- Second quadrant: Only \(\sin\) is positive between \(90^\circ\) and \(180^\circ\).
- Third quadrant: Only \(\tan\) is positive between \(180^\circ\) and \(270^\circ\).
- Fourth quadrant: Only \(\cos\) is positive between \(270^\circ\) and \(360^\circ\).
- The angle is measured from the positive x-direction.
- An anticlockwise rotation is taken as positive, and a clockwise rotation is taken as negative.
- The acute angle made with the x-axis is sometimes called the basic angle or the reference angle.
Tip: To memorize this diagram, “All Students Trust Cambridge”.
5.3 Graphs of trigonometric functions
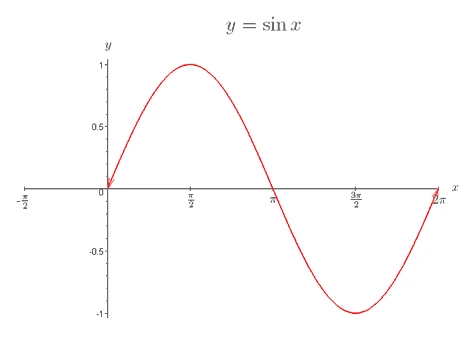
- The graph of \(\sin x\):
- The graph of \(\cos x\):
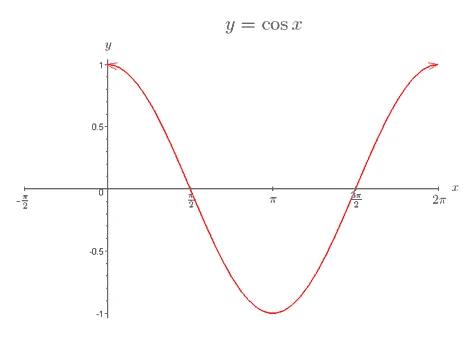
- The sine and cosine functions are called periodic functions because they repeat themselves over and over again.
- The period of a periodic function is defined as the length of one cycle.
- The sine and cosine functions repeat every \(360^\circ\).
- The amplitude of a periodic function is defined as the distance between a maximum (or minimum) point and the principal axis.
- The functions \(y = \sin x\) and \(y = \cos x\) both have amplitude 1.
- The symmetry of the curve \(y = \sin x\) shows these important relationships:
- \(\sin(-x) = -\sin(x)\)
- \(\sin(180^\circ – x) = \sin(x)\)
- \(\sin(180^\circ + x) = -\sin(x)\)
- \(\sin(360^\circ – x) = -\sin(x)\)
- \(\sin(360^\circ + x) = \sin(x)\)
- The graph of \(\tan x\):
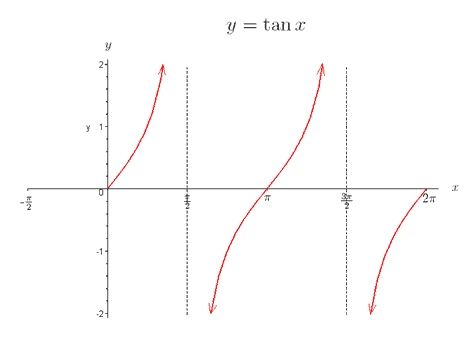
- The tangent function repeats its cycle every \(180^\circ\), so its period is \(180^\circ\).
- There are asymptotes in the tangent function. The branches of the graph get closer and closer to the asymptotes without ever reaching them.
- Asymptotes are found at \(x = 90^\circ\), \(x = 270^\circ\), and \(x = 450^\circ\).
- The tangent function does not have an amplitude.
Transformations of trigonometric functions
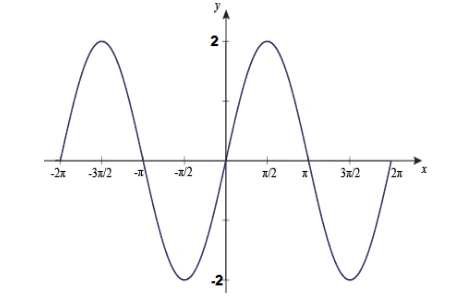
- The graph of \( y = a\sin(x) \):
-
- The equation for the graph: \( y = 2\sin(x) \)
- Comparison of the graph \( y = \sin(x) \) and \( y = 2\sin(x) \):
- The graph of \( y = 2\sin(x) \) is a stretch of the graph of \( y = \sin(x) \).
- It is a stretch, stretch factor 2, parallel to the y-axis.
- The amplitude of \( y = 2\sin(x) \) is 2 and the period is 360°.
- The graph of \( y = \sin(ax) \):
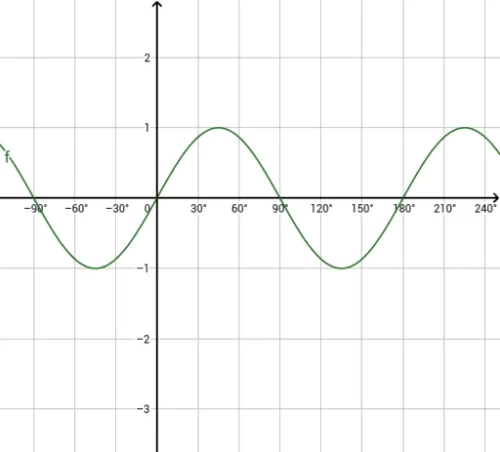
-
- The equation for the graph: \( y = \sin(2x) \)
- Comparison of the graph \( y = \sin(x) \) and \( y = \sin(2x) \):
- The graph of \( y = \sin(2x) \) is also a stretch of the graph of \( y = \sin(x) \).
- It is a stretch, stretch factor \( \frac{1}{2} \), parallel to the x-axis.
- The amplitude of \( y = \sin(2x) \) is 1 and the period is 180°.
- The graph of \( y = a + \sin(x) \):
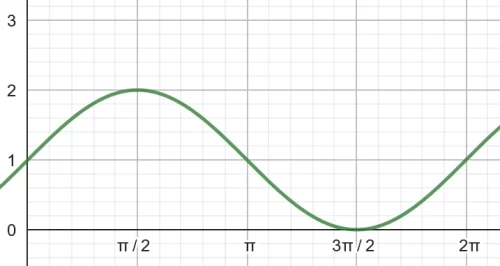
-
- The equation for the graph: \( y = 1 + \sin(x) \)
- Comparison of the graph \( y = \sin(x) \) and \( y = 1 + \sin(x) \):
- The graph of \( y = 1 + \sin(x) \) is a translation of the graph of \( y = \sin(x) \).
- It is a translation of 1 unit upward.
- The amplitude of \( y = 1 + \sin(x) \) is 1 and the period is 360°.
- The graph of \( y = \sin(x + a) \):
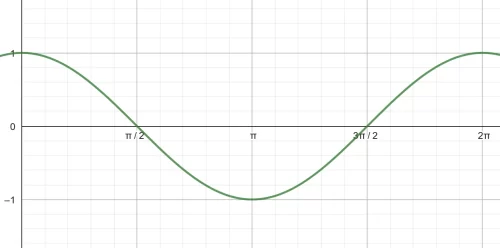
-
- The equation for the graph: \( y = \sin(x + 90) \)
- Comparison of the graph \( y = \sin(x) \) and \( y = \sin(x + 90) \):
- The graph of \( y = \sin(x + 90) \) is a translation of the graph of \( y = \sin(x) \).
- It is a translation of -90° parallel to the x-axis.
- The amplitude of \( y = \sin(x + 90) \) is 1 and the period is 360°.
5.4 Inverse trigonometric functions
- The graph of \( y = \sin^{-1}(x) \):
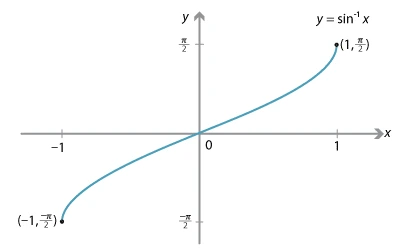
-
- Domain: -1 ≤ x ≤ 1
- Range: -π/2 ≤ y ≤ π/2
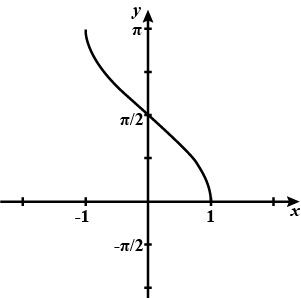
- The graph of y = \cos^{-1}(x):
-
- Domain: -1 ≤ x ≤ 1
- Range: 0 ≤ y ≤ π
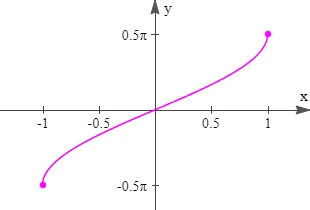
- The graph of y = \tan^{-1}(x):
-
- Domain: x ∈ ℝ
- Range: -π/2 < y < π/2
5.5 Trigonometric Equations
- Trigonometric identities are used to simplify trigonometric equations before solving them.
- The two identities you must know are:
- \( \tan(x) = \frac{\sin(x)}{\cos(x)} \)
- \( \sin^2(x) + \cos^2(x) = 1 \)
- Derivation of the identities:
- \( \tan(x) = \frac{\text{Opposite}}{\text{Adjacent}} \)
- \( \frac{\sin(x)}{\cos(x)} = \frac{\left(\frac{\text{Opposite}}{\text{Hypotenuse}}\right)}{\left(\frac{\text{Adjacent}}{\text{Hypotenuse}}\right)} = \frac{\text{Opposite}}{\text{Adjacent}} = \tan(x) \)
- \( \cos^2(x) + \sin^2(x) = 1 \)
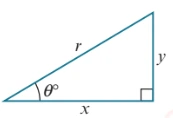
\( x^2 + y^2 = r^2 \)
\( \left( \frac{x}{r} \right)^2 + \left( \frac{y}{r} \right)^2 = 1 \), as \( \cos(\theta) = \frac{x}{r} \) and \( \sin(\theta) = \frac{y}{r} \)
🔥 Approach to solve trigonometric equations:
- Sketching a graph
- Using trigonometric identities
- Using the CAST diagram
- Factorising quadratic trigonometric equations
