6. Geometry and Trigonometry

SAT Math

Written by: Pranav I
Formatted by: Rithanya S

The Digital SAT will have 6 to 7 geometry and trigonometry questions in the two Math modules
The reference sheet will contain some of what you’ll need to tackle geometry on the Digital SAT
It can be opened by clicking the Reference button in the upper right corner of the screen

🔥 The GEOMETRY Basic Approach

Draw a figure on your scratch paper. If the question contains the note “Figure not drawn to scale”, draw the figure using information in the question.
Label the figure with any information given in the question. Sometimes you can plug in for parts of the figure as well.
Write down formulas that you might need for the question.
Ballpark if you’re stuck or running out of time.

LINES AND ANGLES

A circle contains 360 degrees.
When you think about angles, remember circles.
A line is a 180° angle.
When two lines intersect, four angles are formed.
When two lines intersect, the angles opposite each other will have the same measures; these angles are known as VERTICLE ANGLES.
If two lines are perpendicular to each other, each of the four angles formed is 90°; a 90° angle is called a RIGHT ANGLE. Never assume two lines are perpendicular unless told so.
When two parallel lines are cut by a third line, all of the small angles are equal, all of the big angles are equal, and the sum of any big angle and any small angle is 180°. Never assume two lines are parallel until told so.

TRIANGLES

Every triangle contains three interior angles that add up to 180°.
An isosceles triangle is one in which two of the sides are equal in length. The angle opposite these equal sides are also equal.
An equilateral triangle is one in which all three sides and angles are equal in length. An angle in an equilateral triangle is equal to 60°.
A right triangle is a triangle in which one of the angles is a right angle (90°). The longest side of the right triangle opposite the right angle is called the HYPOTENUSE; the other two sides are called the LEGS. The angles in an isosceles right triangle always measure 45°, 45° and 90°.
The perimeter of a triangle is the sum of the length of its sides.
The area of a triangle is 0.5(base x height).

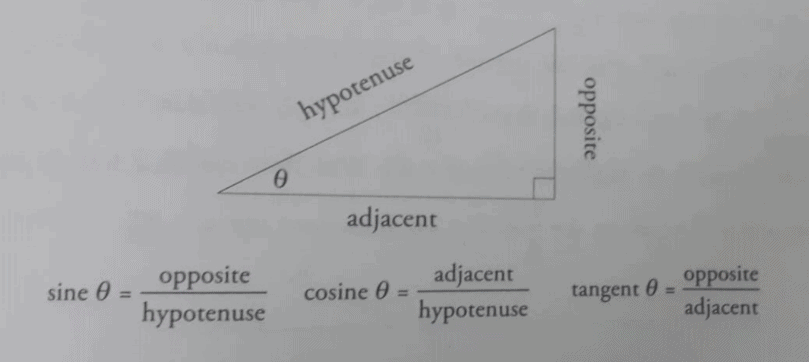
Pythagorean Theorem

In a right triangle, the square of the hypotenuse equals the sum of the squares of the other two sides.
a² + b² = c²

SOH CAH TOA

Special Right Triangles

Most geometry questions involving right triangles tend to focus on certain relationships
Two triangles with sides ratios, known as the Pythagorean triples, are the test-writers’ favorites
One has side lengths (3-4-5)
One has side lengths (5-12-13)
The test-writers might also use right triangles with sides that are multiples of the common Pythagorean triples
There are another pair of right triangles with a specific ratio of angles
- 30°-60°-90° triangle
- 45°-45°-90° triangle (this is an isosceles triangle with the same leg lengths)
The sides of these triangles always have the same fixed ratio to each other

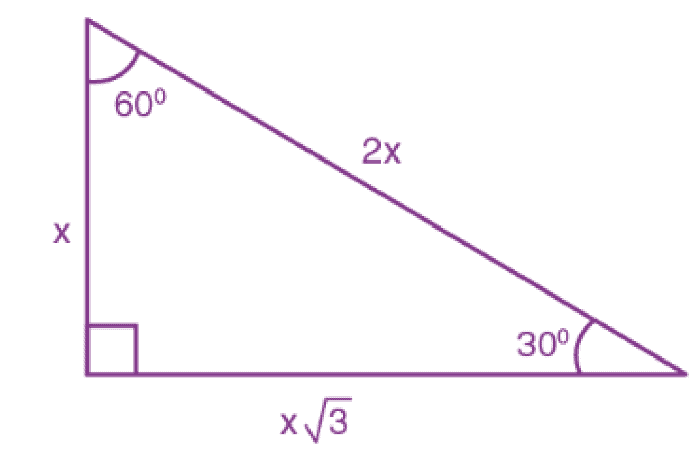
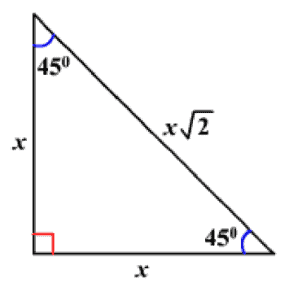
NOTE: This information is included in the reference sheet

Similar and Congruent Triangles

Similar triangles have the same shape but not the same size
- Their angles are identical
- Their corresponding sides (sides that correspond to the same angle) have the same ratio
Two triangles are similar when at least one of the following is true:
- All three angles of the triangles are congruent (AAA).
- Pairs of sides of the triangles are in proportion, and the angle in between those sides is congruent (SAS).
- All three sides of one triangle are in proportion to the corresponding three sides of the other triangle (SSS).

Congruent triangles have the same shape and size
- Their angles are identical
- Their corresponding sides are also identical
Two triangles are congruent when at least one of the following is true:
- All three sides are equal (SSS).
- Two pairs of angles and the side between them are equal (ASA).
- Two pairs of sides and the angle between them are equal (SAS).
- Two pairs of angles and a side that isn’t between them are equal (AAS).

Similar Triangles and Trigonometry

If two triangles are similar, corresponding trigonometric functions are equal, as the side lengths are proportional.

CIRCLES

The circumference of a circle is 2πr or πd, where r is the radius of the circle and d is the diameter. Therefore, the diameter is twice the length of the radius. (Feel free to leave your work in terms of π, as the answer choices will be in specific form)
The area of a circle is r², where r is the radius of the circle.
A tangent is a line that touches a circle at exactly one point. A radius drawn from that tangent point forms a 90° angle with the tangent.
NOTE: If a question refers to Circle R, it means the centre of the circle is Point R.

Converting Degrees to Radians

Some geometry questions ask the test-takers to convert an angle measurement from degrees to radians
180° = π radians
NOTE: This relationship is included in the reference sheet

Arcs and Sectors

Arcs are a portion of the circumference
Sectors are portions of the area
Both arcs and sectors have the same relationship with the circle, based on the central angle
The central angle is the angle at the center of the circle that creates the arc or sector
Arcs and sectors are proportional to the circumference and area, respectively, as the central angle is to 360°
A minor arc or sector has a central angle that is less than 180°
A major arc or sector has a central angle that is more than 180°

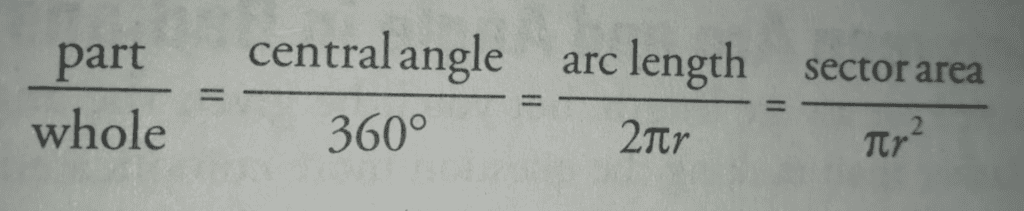
Relationship Between Arc and Angle in Radians

s = rθ
- s is the arc length
- r is the radius
- θ is the central angle in radians

RECTANGLES AND SQUARES

The perimeter of a rectangle is the sum of the lengths of its sides.
The area of a rectangle is length x width.
A square is a rectangle whose four sides are all equal in length. The perimeter of a square is four times the length of any side; the area is the length of any side squared.
In rectangles and squares all angles are right angles (90°).

VOLUME

The reference sheet in the testing app contains all the formulas you will ever need for volume questions on the Digital SAT. Simply apply the Geometry Basic Approach using the given formulas to ace any and all volume questions!

BALLPARKING

Helps you avoid careless mistakes by immediately eliminating answers that could not possibly be correct

🔥 Tip

Before you begin working out, look at the drawing in the question and make a rough estimate of the answer based on the given information

How High Is the Ceiling?

Your Ballpark answer wouldn’t be exact, but it would be close.

PLUGGING IN

Plug in values for missing information and then use the results either to find the answer directly or to eliminate answers that cannot be correct.